The University of Texas at Dallas                       Erik Jonsson School of Engineering and 
                                                                               Computer Science 
            Simplifying Logic Circuits  with Karnaugh Maps 
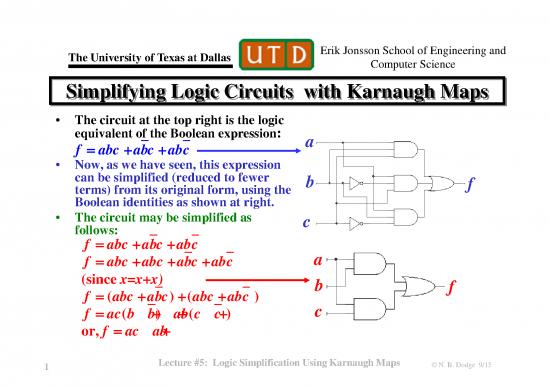
         •    The circuit at the top right is the logic 
              equivalent of the Boolean expression:              a 
                   
              f =abc ++abc        abc  
         •    Now, as we have seen, this expression 
              can be simplified (reduced to fewer                b                                   f 
              terms) from its original form, using the 
              Boolean identities as shown at right.   
         •    The circuit may be simplified as                  c 
              follows:  
                f =abc ++abc        abc                            a 
                f =abc +abc ++abc           abc  
               (since x=x+x)                                       b                             f 
                f =(abc +abc) +(abc +abc )                         c 
                f =ac(b b++)        ab(c     c+ ) 
               or, f =ac       ab+ 
       1                        Lecture #5:  Logic Simplification Using Karnaugh Maps        © N. B. Dodge  9/15 
            The University of Texas at Dallas                       Erik Jonsson School of Engineering and 
                                                                               Computer Science 
                          Simplifying Logic Circuits (2) 
          •    Since you have now had some                       a 
               experience with simplification of 
               Boolean expressions, this                         b                                   f 
               example is (hopefully) familiar 
               and understandable.                              c 
          •    However, for more complex 
               Boolean expressions, the                           Original logic circuit 
               identity/substitution approach                      a 
               can be VERY cumbersome (at                          b 
               least, for humans).                                                               f 
          •    Instead of this approach, we can                    c 
               use a graphical technique called 
               the Karnaugh map.                            Simplified equivalent logic circuit    
       2                     Lecture #5:  Logic Simplification Using Karnaugh Maps           © N. B. Dodge  9/15 
                   The University of Texas at Dallas                                                        Erik Jonsson School of Engineering and 
                                                                                                                              Computer Science 
                                                                Karnaugh Maps 
             •      Another approach to simplification is                                                                          yy    
                    called the Karnaugh map, or K-map.   
             •       A K-map is a truth table graph, which                                                           x 00            01 
                    aids in visually simplifying logic.                                                                       0             1            This minterm 
                                                                                                                                                                                                                  
             •      It is useful for up to 5 or 6 variables, and                                                              10           11            is expressed as 
                                                                                                                                                                                 .  
                    is a good tool to help understand the                                                            x                                      f = xy
                    process of logic simplification.                                                                          2             3 
             •      The algebraic approach we have used                                                              Two-Variable K-map, 
                    previously is also used to analyze complex                                                       labeled for SOP terms.   
                    circuits in industry (computer analysis).                                                        Note the four squares  
             •      At the right is a 2-variable K-map.                                                              represent all the com- 
             •      This very simple K-map demonstrates                                                              binations of the two  
                    that an n-variable K-map contains all the                                                        K-map variables, or 
                    combination of the n variables in the K-                                                         minterms, in x & y 
                    map space.                                                                                       (example above). 
           3                                       Lecture #5:  Logic Simplification Using Karnaugh Maps                                           © N. B. Dodge  9/15 
            The University of Texas at Dallas                       Erik Jonsson School of Engineering and 
                                                                               Computer Science 
                        Three-Variable Karnaugh Map 
       •    A useful K-map is one of three variables.   
       •    Each square represents a 3-variable                              yz  yzy   zy   z
            minterm or maxterm.                                            000         001         011          010 
       •    All of the 8 possible 3-variable terms are  x 0             1             3              2        
            represented on the K-map.   
       •    When moving horizontally or vertically,                   x 100         101          111         110 
            only 1 variable changes between adjacent                       4             5             7              6         
            squares, never 2.  This property of the K-
            map,  is unique and accounts for its 
            unusual numbering system.                                       As an example, this 
       •    The K-map shown is one labeled for SOP                          minterm cell (011) 
            terms.  It could also be used for a POS                         represents the 
                                                                            minterm                .   
            problem, but we would have to re-label                                     f = xyz
            the variables.   
       4                     Lecture #5:  Logic Simplification Using Karnaugh Maps           © N. B. Dodge  9/15