968                                                                                                           Chapter 9 Quadratic Equations and Functions
                            9.8    Solve Quadratic Inequalities
                          Learning Objectives
                          By the end of this section, you will be able to:
                               Solve quadratic inequalities graphically
                               Solve quadratic inequalities algebraically
                            Be Prepared!
                               Before you get started, take this readiness quiz.
                                     1.   Solve: 2x − 3 = 0.
                                          If you missed this problem, review Example 2.2.
                                     2.   Solve: 2y2 + y = 15.
                                          If you missed this problem, review Example 6.45.
                                     3.   Solve           1         >0
                                                    2
                                                   x +2x−8
                                          If you missed this problem, review Example 7.56.
                          Wehavelearnedhowtosolvelinearinequalities and rational inequalities previously. Some of the techniques we used to
                          solve them were the same and some were different.
                          Wewillnowlearntosolveinequalities that have a quadratic expression. We will use some of the techniques from solving
                          linear and rational inequalities as well as quadratic equations.
                          We will solve quadratic inequalities two ways—both graphically and algebraically.
                          Solve Quadratic Inequalities Graphically
                          Aquadratic equation is in standard form when written as ax2 + bx + c = 0. If we replace the equal sign with an inequality
                          sign, we have a quadratic inequality in standard form.
                            Quadratic Inequality
                            Aquadratic inequality is an inequality that contains a quadratic expression.
                            The standard form of a quadratic inequality is written:
                                                                                   2                                2
                                                                               ax +bx+c<0                       ax +bx+c≤0
                                                                                   2                                2
                                                                               ax +bx+c>0                       ax +bx+c≥0
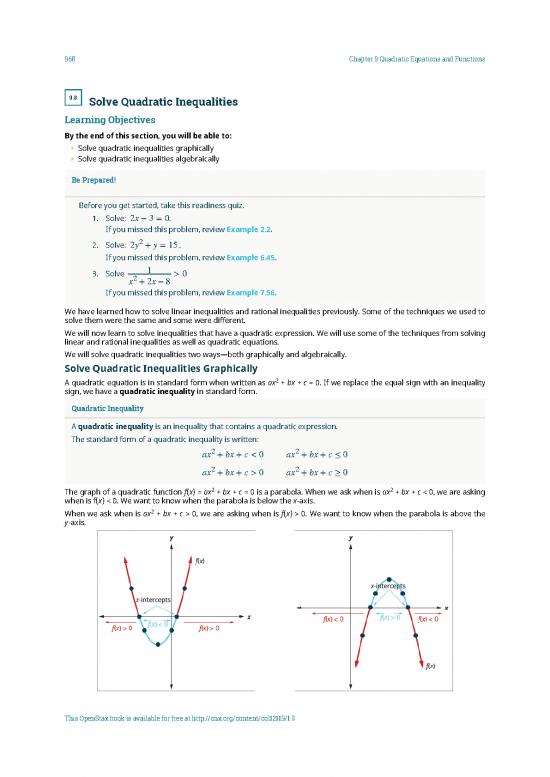
                          Thegraphofaquadraticfunction f(x) = ax2 + bx + c = 0 is a parabola. When we ask when is ax2 + bx + c < 0, we are asking
                          when is f(x) < 0. We want to know when the parabola is below the x-axis.
                          Whenweaskwhenisax2+bx+c>0,weareaskingwhenisf(x)>0.Wewanttoknowwhentheparabolaisabove the
                          y-axis.
                          This OpenStax book is available for free at http://cnx.org/content/col12119/1.3
                Chapter 9 Quadratic Equations and Functions                                                       969
                  EXAMPLE 9.64  HOW TO SOLVE A QUADRATIC INEQUALITY GRAPHICALLY
                Solve x2 − 6x + 8 < 0 graphically. Write the solution in interval notation.
                    Solution
           970                                          Chapter 9 Quadratic Equations and Functions
           This OpenStax book is available for free at http://cnx.org/content/col12119/1.3
                     Chapter 9 Quadratic Equations and Functions                                                                                       971
                                                              2
                           TRY IT : : 9.127       ⓐSolve x +2x−8<0 graphically andⓑwrite the solution in interval notation.
                           TRY IT : : 9.128       ⓐSolve x2−8x+12≥0 graphically andⓑwrite the solution in interval notation.
                     We list the steps to take to solve a quadratic inequality graphically.
                                  HOW TO : : SOLVE A QUADRATIC INEQUALITY GRAPHICALLY.
                                  Step 1.   Write the quadratic inequality in standard form.
                                  Step 2.                                     2
                                            Graph the function f(x) = ax + bx + c.
                                  Step 3.   Determine the solution from the graph.
                     In the last example, the parabola opened upward and in the next example, it opens downward. In both cases, we are
                     looking for the part of the parabola that is below the x-axis but note how the position of the parabola affects the solution.
                       EXAMPLE 9.65
                     Solve −x2−8x−12 ≤ 0 graphically. Write the solution in interval notation.
                          Solution
                       The quadratic inequality in standard form.                                         2
                                                                                                      −x −8x−12≤0
                                                           2                         The parabola opens downward.
                       Graph the function f(x) = −x −8x−12.
                       Find the line of symmetry.                                                   b
                                                                                           x = −
                                                                                                   2a
                                                                                                     −8
                                                                                           x = −
                                                                                                   2(−1)
                                                                                           x = −4
                       Find the vertex.                                                             2
                                                                                        f (x) = −x −8x−12
                                                                                                        2
                                                                                      f (−4) = −(−4) −8(−4)−12
                                                                                      f (−4) = −16 + 32 − 12
                                                                                      f (−4) = 4
                                                                                              (       )
                                                                                     Vertex −4, 4