Filetype PDF | Posted on 27 Jan 2023 | 2 years ago
Authentication
digital resources
145x Filetype PDF File size 2.23 MB Source: www.rbrhs.org
Precalculus
Name: ___________________________ Teacher: _______________
Block: ______
1.3 The Graphs of Functions: Notes, Examples, and Practice Problems
● The set of all possible inputs (xvalues) of a function is called the domain of a
function.
● The set of all the possible outputs (yvalues) of a function is called the range of a
function.
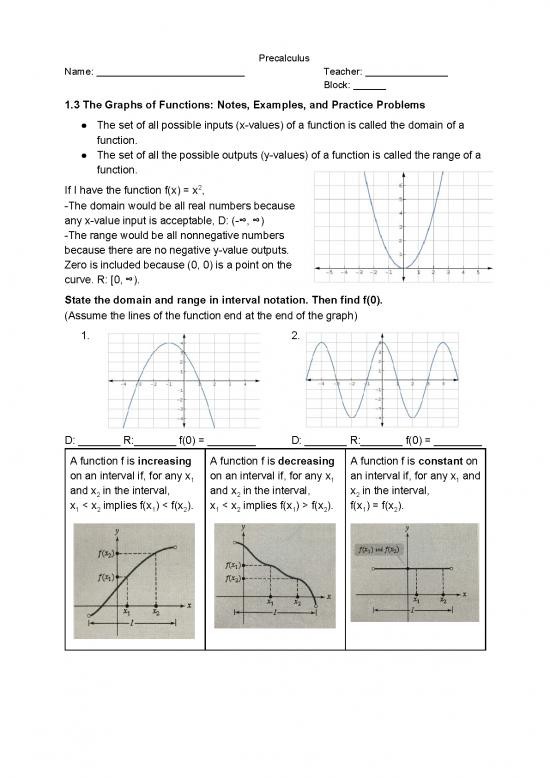
2
If I have the function f(x) = x,
The domain would be all real numbers because
any xvalue input is acceptable, D: (∞, ∞)
The range would be all nonnegative numbers
because there are no negative yvalue outputs.
Zero is included because (0, 0) is a point on the
curve. R: [0, ∞).
State the domain and range in interval notation. Then find f(0).
(Assume the lines of the function end at the end of the graph)
1. 2.
D: _______ R:_______ f(0) = ________ D: _______ R:_______ f(0) = ________
A function f is increasing A function f is decreasing A function f is constant on
on an interval if, for any x on an interval if, for any x an interval if, for any x and
1 1 1
and x in the interval, and x in the interval, x in the interval,
2 2 2
x < x implies f(x) < f(x). x < x implies f(x) > f(x). f(x) = f(x).
1 2 1 2 1 2 1 2 1 2
Precalculus
Name: ___________________________ Teacher: _______________
Block: ______
State the interval on which the graph is increasing, decreasing, or constant.
(Assume the lines of the function continue to negative and positive infinity)
3. 4.
Increasing: _____________ Increasing: _____________
Decreasing: ____________ Decreasing: ____________
Constant: ______________ Constant: ______________
A function value f(a) is called A function value f(a) is called
a relative minimum of f if a relative maximum of f if
there exists an interval there exists an interval (x, x)
1 2
(x, x) that contains a such that contains a such that
1 2
that
x < x < x implies f(a) ≥ f(x)
1 2
x < x < x implies f(a) ≤ f(x)
1 2
English translation: a point
English translation: a point on the graph that has the
on a graph that has the lowest yvalue relative to
highest yvalue relative to the points around it (valley)
the points around it (peak)
3
Given the graph f(x) = x 3x (to the right)
The relative maximum will be the point (1, 2).
The relative minimum will be the point (1, 2)
Precalculus
Name: ___________________________ Teacher: _______________
Block: ______
Use the graph to answer the following questions.
5.
a. Indicate the interval(s) of which f is increasing. ________
________________________________________________
b. Indicate the interval(s) of which f is decreasing. ________
________________________________________________
c. Identify the relative maximum. _________
d. Identify the relative minimum. __________
e. State the domain and range in interval notation._____________________________
3
Given the function, f(x) = x + x, it is not
so easy to estimate the relative
maximums and minimums. We are able
to approximate these using a graphing
calculator.
Plug the equation into your calculator and
set the window similar to the image to the
right. Hit the blue 2nd key then the CALC
(TRACE) key.
To find the minimum, choose number 3:
minimum. It will say “Left Bound?” (similar
to finding a zero) You will move the
cursor to the left of where you think the
relative minimum is and hit ENTER.
Now it will say “Right Bound?” Move the
cursor to the right of where you think the
relative minimum is and hit ENTER.
Next it will say “Guess?” Check that your
Left and Right Bounds are accurate and
hit ENTER. The relative minimum is
(.5777, .385).
Precalculus
Name: ___________________________ Teacher: _______________
Block: ______
To find the maximum, choose number 4:
maximum. Repeat the same steps of
setting the Left and Right Bound. The
relative maximum is (.5777, .385)
Use a graphing utility to approximate any relative maximum or minimum values.
3 2
6. f(x) = 2x + 3x 12x Rel. Min. _________ Rel. Max. __________
2
7. f(x) = x + 7x Rel. Min. _________ Rel. Max. __________
8. Answer the following:
a. the domain of f ________________________
b. the range of f _________________________
c. the xintercepts _______________________
d. the yintercept ________________________
e. intervals on which f is increasing __________
_____________________________________
f. intervals on which f is decreasing ___________
______________________________________
g. values of x for which f(x) ≤ 0 ______________
____________________________________
h. the numbers at which f has a relative maximum
_____________________________________
i. the relative maxima of f __________________
j. f(2) _________________________________
k. the values of x for which f(x) = 0 ___________
no reviews yet
Please Login to review.
