139x Filetype PDF File size 0.74 MB Source: webstor.srmist.edu.in
DEPARTMENT OF MATHEMATICS
FACULTY OF ENGINEERING AND TECHNOLOGY
SRM UNIVERSITY
SEMESTER I MA1011- MATRICES AND CALCULUS ACADEMIC YEAR: 2014-2015
LECTURE SCHEME / PLAN
The objective is to equip the students of Engineering and Technology, the knowledge of
Mathematics and its applications so as to enable them to apply them for solving real world problems.
The list of instructions (provided below) may be followed by a faculty relating to his/her own
schedule includes warm-up period, controlled/free practice, and the respective feedback of the
classes who handle. The lesson plan has been formulated based on high quality learning outcomes
and the expected outcomes are as follows
Each subject must have a minimum of 56 hours, which in turn, 45 hours for lecture and rest of
the hours for tutorials. The faculty has to pay more attention in insisting the students to have 95
% class attendance.
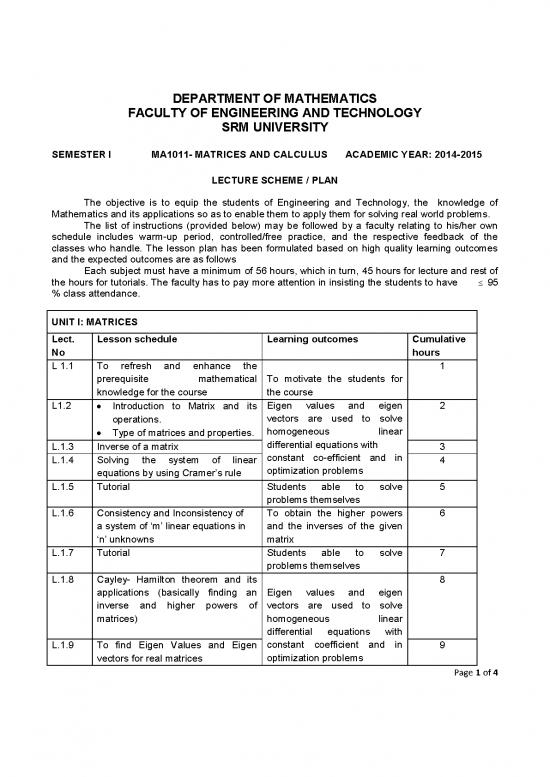
UNIT I: MATRICES
Lect. Lesson schedule Learning outcomes Cumulative
No hours
L 1.1 To refresh and enhance the 1
prerequisite mathematical To motivate the students for
knowledge for the course the course
L1.2 Introduction to Matrix and its Eigen values and eigen 2
operations. vectors are used to solve
homogeneous linear
Type of matrices and properties.
differential equations with
L.1.3 Inverse of a matrix 3
constant co-efficient and in
L.1.4 Solving the system of linear 4
optimization problems
equations by using Cramer’s rule
L.1.5 Tutorial Students able to solve 5
problems themselves
L.1.6 Consistency and Inconsistency of To obtain the higher powers 6
a system of ‘m’ linear equations in and the inverses of the given
‘n’ unknowns matrix
L.1.7 Tutorial Students able to solve 7
problems themselves
L.1.8 Cayley- Hamilton theorem and its 8
applications (basically finding an Eigen values and eigen
inverse and higher powers of vectors are used to solve
matrices) homogeneous linear
differential equations with
L.1.9 To find Eigen Values and Eigen constant coefficient and in 9
vectors for real matrices optimization problems
Page 1 of 4
L.1.10 Properties of Eigen values and 10
Eigen vectors.
L.1.11 Problems based on the Students able to solve 11-12
Properties problems themselves
Tutorial
CYCLE TEST – I : DATE: 18.08.2014
UNIT II: TRIGONOMETRY
L.2.1 Review of complex numbers 13
To get familiar with hyperbolic,
L.2.2 DeMoivre’s theorem and its 14-15
exponential and trigonometric
Applications
functions
Expansion of sinnθ and cosnθ
interms of sinθ & cosθ
L.2.3 Tutorial Students able to solve 16
problems themselves
4L.2.4 Expansion of tannθ interms of To get familiar with hyperbolic, 17-18
tanθ exponential and trigonometric
L.2.5 Expansion of sinnθ & cosnθ interms functions 19
of series of sines and cosines of
multiples of θ
L.2.6 Tutorial Students able to solve 20
problems themselves
L2.7 Hyperbolic functions To get familiar with hyperbolic, 21
L.2.8 Inverse hyperbolic functions exponential and trigonometric 22
functions
L.2.9 Tutorial Students able to solve 23
problems themselves
CYCLE TEST – II : DATE: 19.09.2014
UNIT III: DIFFERENTIAL CALCULUS
L.3.1 Brief overview of Differential 24
calculus and the geometry behind
it. To get familiar with the
L.3.2 Derivatives from first functions of several variables 25
Principles(Delta method)
L.3.3 Derivatives by applying rules 26
L.3.4 Tutorial Students able to solve 27
problems themselves
L.3.5 Differentiation of implicit 28
function
L.3.6 Differentiation of parametric To get familiar with the 29
functions functions of several variables
L.3.7 Successive differentiation – 30
second order derivatives
Page 2 of 4
L.3.8 Finding nth order derivative 31
using mathematical induction
L.3.9 Leibnitz theorem for the nth To get familiar with the 32-33
L.3.10 derivative of a product functions of several variables
L.3.11 Tutorial Students able to solve 34
problems themselves
SURPRISE TEST
UNIT IV: INTEGRAL CALCULUS
L.4.1 Introduction To have a sound knowledge in 35
types of integration
L.4.2 Integrals of standard function 36
L.4.3 Tutorial Students able to solve 37
problems themselves
L.4.4 Various types of integration To have a sound knowledge in 38-39
L.4.5 types of integration
40
L.4.6 Integration by parts To have a sound knowledge in 41
ax n n
types of integration
L.4.7 Reduction formula for e x , sin x 42-43
L.4.8 Reduction formula for 44-45
n n m
cos x,sin xcos x
L.4.9 Tutorial Students able to solve 46
problems themselves
UNIT V:APPLICATIONS OF DIFFERENTIAL CALCULUS AND INTEGRAL CALCULUS
L.5.1 Application of differential calculus To improve the ability in 47
solving the application of
L.5.2 Tangent and normal 48-49
differential and integral
calculus
L.5.3 Tutorial Students able to solve 50
problems themselves
L.5.4 Radius of curvature To improve the ability in 51-52
solving the application of
L.5.5 Velocity and acceleration differential and 53
integral calculus
L.5.6 Tutorial Students able to solve 54
problems themselves
L.5.7 Integral calculus – Length of a curve To improve the ability in 55
solving the application of
L.5.8 Area under or area between the 56-57
differential and
curves
integral calculus
L.5.9 Tutorial Students able to solve 58
problems themselves
Page 3 of 4
MODEL EXAM 05.11.2014 (Duration: 3 Hours)
LAST WORKING DAY : 21.11.2014
TEXT BOOKS:
th
Kreyszig. E, Advanced Engineering Mathematics, 10 edition, John Wiley & Sons, Singapore,
2012
Dr. K. Ganesan, Dr. Sundarammal Kesavan, Prof. K. S. Ganapathy Subramanian, Dr. V.
th
Srinivasan, Matrices and Calculus, Gamma Publications, 6 Edition, 2014.
REFERENCES
nd
Grewal B. S, Higher Engg Maths, Khanna Publications, 42 Edition.2012.
th
Veerarajan T., Engineering Mathematics, Tata McGraw Hill Publishing Co., New Delhi, 5
Edition, 2006
th
Kandasamy P etal. Engineering Mathematics, Vol. I (4 revised edition), S. Chand & Co., New
Delhi, 2000.
Narayanan S., Manicavachagom Pillay T. K., Ramanaiah G., Advanced Mathematics for
Engineering students, Volume I (2nd edition), S. Viswanathan Printers and Publishers, 1992
nd
Venkataraman M.K., Engineering Mathematics – First Year (2 edition), National Publishing
Co., Chennai,2000.
th
David E.Penney and C.Henry Edwards, Single Variable Calculus, Prentice Hall; 6 edition,
2002.
WEB BASED RESOURCES
http://www.the-science-lab.com/Math/
http://botw.org/top/Science/Math/
http://dir.yahoo.com/Science/Mathematics/
http://www.cms.caltech.edu/
Internal marks Total: 50
Internal marks split up: Cycle Test 1: 10 Marks Model Exam: 20 Marks
Cycle Test 2: 10 Marks Surprise Test: 5 marks
Attendance: 5 marks
Dr. B.Vennila Dr. K. Ganesan
Assistant Professor(S.G) Professor & Head
Course Co-ordinator Department of Mathematics
Email: vennila.b@ktr.srmuniv.ac.in Email: hod.maths@ktr.srmuniv.ac.in
Tel: +91-44-27417000 Ext: 2706 Tel: +91-44-27417000 Ext: 2701
Page 4 of 4
no reviews yet
Please Login to review.