211x Filetype PDF File size 0.28 MB Source: teachers.henrico.k12.va.us
AP Calculus AB
Syllabus
Course Overview:
At this school, we cover everything in the Calculus AB topic outline as it appears in the
AP Calculus Course Description, including partial fractions, integration by parts, and
L’Hopital’s Rule. The textbook used for this class is Calculus: Graphical, Numerical,
Algebraic, 3rd ed. AP edition, By Finney, Demana, Waits, Kennedy. The main objectives
for the course are that students will be properly prepared for success on the AP exam and
in subsequent mathematics courses. There is an attempt to balance mastery of concepts,
critical thinking, and integration of technology.
Course Planner:
Below is the sequence of our AP Calculus course.
High School Mathematics AB
AP Calculus Course Outline – 47 minute periods
Textbook: Calculus: Graphical, Numerical, Algebraic, by Finney, et al. 2007
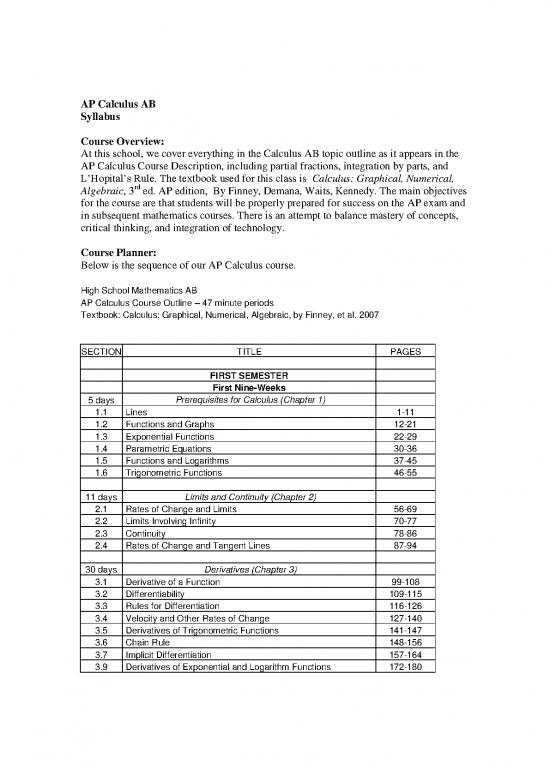
SECTION TITLE PAGES
FIRST SEMESTER
First Nine-Weeks
5 days Prerequisites for Calculus (Chapter 1)
1.1 Lines 1-11
1.2 Functions and Graphs 12-21
1.3 Exponential Functions 22-29
1.4 Parametric Equations 30-36
1.5 Functions and Logarithms 37-45
1.6 Trigonometric Functions 46-55
11 days Limits and Continuity (Chapter 2)
2.1 Rates of Change and Limits 56-69
2.2 Limits Involving Infinity 70-77
2.3 Continuity 78-86
2.4 Rates of Change and Tangent Lines 87-94
30 days Derivatives (Chapter 3)
3.1 Derivative of a Function 99-108
3.2 Differentiability 109-115
3.3 Rules for Differentiation 116-126
3.4 Velocity and Other Rates of Change 127-140
3.5 Derivatives of Trigonometric Functions 141-147
3.6 Chain Rule 148-156
3.7 Implicit Differentiation 157-164
3.9 Derivatives of Exponential and Logarithm Functions 172-180
Second Nine-Weeks
4 days Derivatives (Chapter 3)
3.9 Derivatives of Exponential and Logarithm Functions 172-180
3.8 Derivatives of Inverse Trigonometric Functions 165-171
32 days Applications of Derivatives (Chapter 4)
4.6 Related Rates 246-255
4.1 Extreme Values of Functions 187-195
4.2 Mean Value Theorem 196-204
4.3 Connection f' and f'' with the graph of f 205-218
4.4 Modeling and Optimization 219-232
8.1 L’Hopital’s Rule
SHOE BOX PROJECT
5 days The Definite Integral (Chapter 5)
5.1 Estimating with Finite Sums 263-273
5.2 Definite Integrals 274-284
2 days EXAM REVIEW
1 day FIRST SEMESTER EXAM
SECOND SEMESTER
Third Nine-Weeks
18 days The Definite Integral (Chapter 5)
5.3 Definite Integrals and Antiderivatives 285-293
5.4 Fundamental Theorem of Calculus 294-305
5.5 Trapezoidal Rule 306-315
13 days Differential Equations and Mathematical Modeling (Chapter 6)
6.1 Antiderivatives and Slope Fields 320-330
6.2 Integration using Chain Rule 331-340
6.3 Integration by Parts 341-348
6.4 Exponential Growth and Decay 350-361
6.5 Logistic Growth 362-372
14 days Applications of Definite Integrals (Chapter 7)
7.1 Integral as Net Change 378-389
7.2 Areas in the Plane 390-398
7.3 Volumes 399-411
7.5 Applications from Science and Statistics 419-429
FOOD VOLUME PROJECT
Fourth Nine-Weeks
10 days Motion (throughout the text)
2 days Derivatives of Inverse Functions 165-170
13 days AP REVIEW
1 day AP EXAM
16 days Preparation for AP Calculus 2
7.3 Shell Method 399-411
7.4 Lengths of Curves 412-418
8.4 Partial Fractions 371 and more
3 days POST AP EXAM PROJECTS
MODEL OF A VOLUME BY CROSS-SECTION
2 days EXAM REVIEW
1 day FINAL EXAM
Teaching Strategies
For a number of students entering Calculus AB, they have had honors level classes before
and are prepared for the rigor of a more advanced class. An electronic webpage
maintained by the teacher shows the pacing guide for the year, clearly indicating the
target date of the AP exam. The teacher works as a coach, with students working as a
team to develop the skills necessary to achieve success on the AP exam. The teacher
offers numerous after school study sessions, including several before semester exams.
Technology and Computer Software
The teacher and students use the TI-89 graphing calculator, as well as the TI-83 or TI-84
calculator in class. Nearly all students have one of these calculators.
A number of powerpoint presentations are incorporated in the class utilizing an
ActivInspire Board. The presentations provide aid in teaching many of the calculus
concepts, such as the definition of the limit. Also, the AP collegeboard website:
http://www.apexvs.com/ApexUI/ is incorporated to enrich understanding.
Student Activities (utilizing the graphing calculator):
In PreCalculus, students learn to find an appropriate viewing window to produce a
complete graph of a function, find the zeros of a function, evaluate a function at a point,
and determine symmetry. These topics are reinforced early in AP Calculus.
Students need to practice using their calculator to solve multiple-choice and free response
questions. A favorite calculator activity is one that helps strengthen the students’
understanding of extrema and concavity. I produce the graph of the derivative on the
calculator and then ask information about the graph of the original function. Students
make the connection between the behaviors of the graphs of f, f′, and f′′.
The following activity was developed to strengthen the student’s understanding of the
limits of functions.
The main objectives in using this lesson is to help students to develop an intuitive
understanding of the nature of limits, lay the foundation for the use of limits in calculus
and to practice evaluating limits graphically, numerically, and algebraically.
In the lab the student studies the behavior of a function f near a specified point. As they
go through the lab they will need to find the limit numerically (using tables on the TI-83
or TI-89 calculator), graphically, or algebraically. The students work in groups of 3 or 4
and all groups have TI-83 and TI-89 owners in them so the students have exposure to
both.
As the students work through the problems, there are a number of higher-order questions
that require the students to write up their conclusions as a group.
LAB: LIMITS OF FUNCTIONS
Goals:
To develop an intuitive understanding of the nature of limits
To lay the foundation for the use of limits in calculus
To evaluate limits graphically, numerically, and algebraically
Procedure
In this lab, we will study the behavior of a function f near a specified
point. While this may be a straightforward process, it can also be very
subtle. In some instances in calculus the process for finding a limit must be
applied carefully. By gaining an intuitive feel for the idea of limits, you will
be laying a solid foundation for success in calculus.
As you go through this lab, evaluate the limits by the method given:
numerically (using table on calculator), graphically, or algebraically. You
might also want to try to use another method as a check and to see how all 3
methods can be used.
x4 1
1. Consider the function f defined by f(x)= x1
a) By successive evaluation of f at x= 1.8, 1.9, 1.99, 1.999, and 1.9999,
what do you think happens to the values of f as x increases towards
2?
no reviews yet
Please Login to review.