183x Filetype PDF File size 0.35 MB Source: brainmatter.com.sg
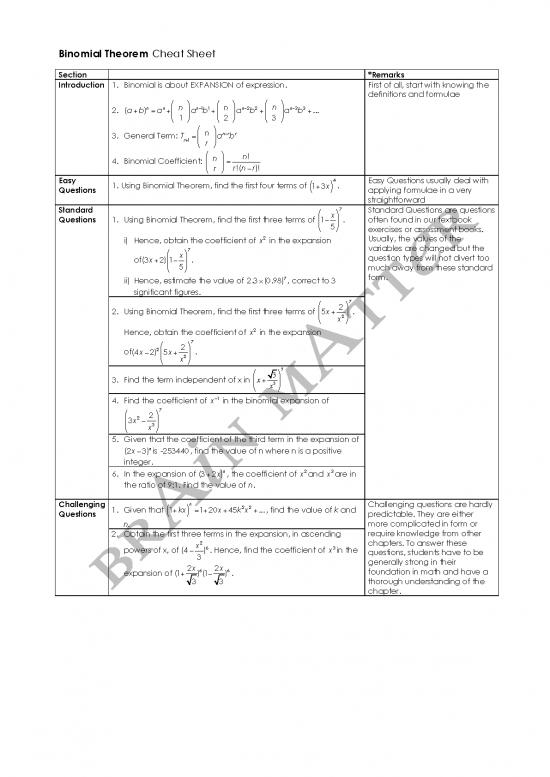
Binomial Theorem Cheat Sheet
Section *Remarks
Introduction 1. Binomial is about EXPANSION of expression. First of all, start with knowing the
definitions and formulae
n n ! n $ n−1 1 ! n $ n−2 2 ! n $ n−3 3
2. (a+b) =a +# &a b +# &a b +# &a b +...
# 1 & # 2 & # 3 &
" % " % " %
! n $ n−r r
3. General Term: T =# &a b
r+1 # r &
" %
! n $ n!
4. Binomial Coefficient: # &=
# r & r!(n−r)!
" %
Easy 1. Using Binomial Theorem, find the first four terms of 1+3x 4. Easy Questions usually deal with
Questions ( ) applying formulae in a very
straightforward
Standard 7 Standard Questions are questions
Questions " x% often found in our textbook
1. Using Binomial Theorem, find the first three terms of $ ' .
1−
$ 5'
# & exercises or assessment books.
i) Hence, obtain the coefficient of x2 in the expansion Usually, the values of the
7 variables are changed but the
" x% question types will not divert too
of $ ' .
(3x+2) 1−
$ 5' much away from these standard
# &
ii) Hence, estimate the value of 7, correct to 3 form.
2.3×(0.98)
significant figures.
7
! 2 $
2. Using Binomial Theorem, find the first three terms of #5x+ & .
# x2 &
" %
Hence, obtain the coefficient of x2 in the expansion
7
2 " 2 %
of(4x−2) $5x+ ' .
$ x2 '
# &
! 3$7
3. Find the term independent of x in #x+ x3 &
" %
4. Find the coefficient of x−1 in the binomial expansion of
7
" 2 2 %
$3x − '
$ x3 '
# &
5. Given that the coefficient of the third term in the expansion of
nis , find the value of n where n is a positive
(2x−3) -253440
integer.
6. In the expansion of n, the coefficient of x2and x3are in
(3+2x)
the ratio of 9:1. Find the value of n.
Challenging 1. Given that 1+kx n =1+20x+45k2x2+..., find the value of k and Challenging questions are hardly
Questions ( ) predictable. They are either
n. more complicated in form or
2. Obtain the first three terms in the expansion, in ascending require knowledge from other
x2 chapters. To answer these
6 x3
powers of x, of (4− 3 ) . Hence, find the coefficient of in the questions, students have to be
2x 2x generally strong in their
6 6 foundation in math and have a
expansion of (1+ ) (1− ) .
3 3 thorough understanding of the
chapter.
no reviews yet
Please Login to review.