227x Filetype PDF File size 0.08 MB Source: tea.texas.gov
Multivariable Calculus
In thermodynamics, we will frequently deal
with functions of more than one variable
e.g., PPT,,Vn, UUT,V,n, UUT,,Pn U = energy
n = # moles
extensive variable: depends on the size of the system
intensive variable: independent of the size of the system
V, n are extensive,
P, T, molar volume V/n are intensive
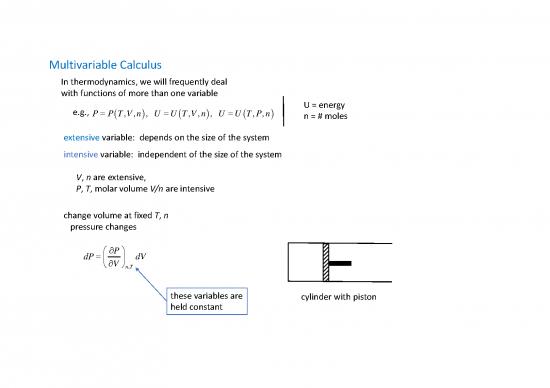
change volume at fixed T, n
pressure changes
P
dP dV
V
nT,
these variables are cylinder with piston
held constant
Suppose we have an ideal gas
PV nRT
PnRT
2
VV
nT, subscripts refer
PnR
to variables that
TV are held constant
Vn,
PRT
nV
VT,
now suppose we want to see how Pchanges when both V and Tchange
PP
Note that this is fully consistent with
dPdV dT
Taylor‐series expansions
V T
Tn,,Vn
If n changes as well
P
dn
need to add a term
n
TV,
In general,
yy x,,xx
12 n
n y
dx x
dy i, ' hold fixed all
n
i1
x' variables except x
i
Ideal gas
PPP
dP dT dV dn
TVn
nV,,Tn T,V
nR nRT RT
dPdT dV dn
2
VVV
for small finite changes
nR nRT RT
PT V n
2
VVV
These equations are most useful when we don't have
an analytical function for the quantity of interest.
Consider
UU (,TP,n)
UUU
dU dT dP dn
TPn
Pn,,Tn T,P
The derivatives are often available experimentally.
We can also write
UU T,,Vn
UUU
dU dT dV dn
TVn
Vn,,Tn T,V
UU
Note, in general,
TT
P,,nVn
no reviews yet
Please Login to review.