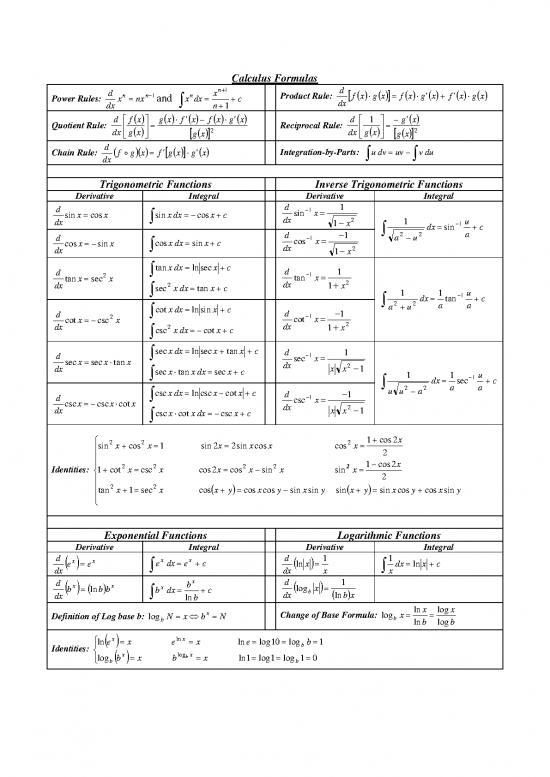
Calculus Formulas 
                                      d    n       n−1            n        xn+1                   Product Rule:  d []() ()                   () () () () 
                  Power Rules:           x =nx         and  ∫x dx =              +c                                   dx f x ⋅ g x = f x ⋅ g' x + f ' x ⋅ g x
                                     dx                                   n+1
                                           ⎡       ⎤                                                                         ⎡       ⎤
                                               () () () () ( )                                                                                 ()
                  Quotient Rule:  d ⎢ f x ⎥ = g x ⋅ f ' x − f x ⋅ g' x                            Reciprocal Rule:  d ⎢ 1 ⎥ = − g' x  
                                       dx g()x                            2                                              dx g()x                2
                                                                  []()                                                                   []()
                                           ⎣       ⎦               g x                                                       ⎣       ⎦    g x
                  Chain Rule:  d (              )()       []() ()                                 Integration-by-Parts:   u dv =uv −              v du  
                                    dx f o g x = f ' g x ⋅ g' x                                                                ∫∫
                                                                                                 
                                   Trigonometric Functions                                                    Inverse Trigonometric Functions 
                           Derivative Integral  Derivative Integral 
                    d sinx = cosx                   ∫sinx dx = −cosx+c                             d sin−1 x =         1      
                   dx                                                                              dx               1−x2             ∫       1       dx =sin−1 u + c  
                    d                                                                              d cos−1 x =        −1                 a2 −u2                   a
                   dxcosx=−sinx                     ∫cosx dx =sinx+c                               dx                1−x2
                    d                               ∫tanx dx = lnsecx +c                           d                  1
                                                                                                           −
                       tan x = sec2 x                                                                  tan 1 x =            
                   dx                               ∫sec2 x dx = tan x + c                         dx             1+x2
                                                                                                                                            1      dx = 1 tan−1 u + c  
                                                      cot x dx = lnsin x + c                                                         ∫ a2 +u2            a         a
                    d                               ∫                                              d       −         −1
                       cot x = −csc2 x                                                                cot 1 x =             
                   dx                               ∫csc2 x dx = −cot x + c                        dx             1+x2
                    d                               ∫secx dx =lnsecx + tan x + c                   d sec−1 x =          1        
                   dx secx =secx⋅tan x                secx⋅tanx dx =secx+c                         dx              x   x2 −1
                                                    ∫                                                                                ∫        1        dx = 1 sec−1 u + c
                                                      cscx dx = lncscx−cotx +c                     d                   −1              u u2 −a2              a         a
                                                                                                           −
                    d cscx = −cscx⋅cotx             ∫                                                 csc 1 x =                  
                   dx                               ∫cscx⋅cotx dx=−cscx+c                          dx              x   x2 −1
                                 ⎧    2           2                                                                      2      1+cos2x
                                  sin    x + cos x =1                 sin 2x = 2sin xcos x                            cos  x =
                                 ⎪                                                                                                   2
                                 ⎪                                                                                              1−cos2x
                                 ⎪         2          2                              2         2                         2
                  Identities:  1+ cot        x = csc x                cos2x = cos      x −sin x                       sin  x =                                     
                                 ⎨                                                                                                   2
                                 ⎪
                                 ⎪tan2 x +1=sec2 x                cos()x + y = cos xcos y − sin xsin y     sin()x + y = sin xcos y + cos xsin y 
                                 ⎪
                                 ⎩
                   
                                     Exponential Functions                                                            Logarithmic Functions 
                           Derivative Integral  Derivative Integral 
                    d     x      x                    ex dx = ex + c                               d (       )   1                     1
                       ()
                   dx e     =e                      ∫                                              dx ln x = x                       ∫ x dx = ln x + c  
                    d     x            x                x        bx                                d (          )      1
                       ()                                                                              log x =                
                        b    =()lnb b               ∫b  dx=           +c                                    b       ()  
                   dx                                            lnb                               dx                lnb x
                  Definition of Log base b: log N = x ⇔bx = N                                     Change of Base Formula: log x = lnx = logx  
                                                        b                                                                                b      lnb     logb
                                 ⎧     x                      ln x
                                     ()
                                  ln e    =x                  e   =x                 ln e = log10 = log    b=1
                  Identities: ⎪                                                                          b        
                                 ⎨         x                  log x
                                 ⎪      ()                       b
                                  logb b      =x              b      =x              ln1= log1= logb 1= 0
                                 ⎩
                                                                                                 
                                                                                                 
                                                            Infinite Series: Definitions & Tests 
                                        ⎧ ∞                           ()
                                        ⎪    an =a +a +a +...   Infinite Series
                                         ∑          1    2     3
                                        ⎪n=
                                        ⎪ 1
                                        ⎪       n                          ()
                     1.        Series: ⎨s =       a =a +a +...+a    nth Partial Sum                      
                                        ⎪ n   ∑ i        1    2         n
                                        ⎪      i=1
                                        ⎪                                   ∞          ()
                                         if  lim sn = s where s∈ℜ then         an = s   Infinite Sum
                                        ⎪   n→∞                            ∑
                                        ⎩                                  n=1
                                                     ∞                                     ⎧ a , if  r  <1
                                                          n                2      3        ⎪
                     2.        Geometric Series:        ar =a+ar+ar +ar +...  =   1−r                              
                                                    ∑                                      ⎨
                                                    n=0                                    ⎪diverges, if  r  ≥1 
                                                                                           ⎩
                                           ∞           converges, if p >1
                     3.        P-Series:       1     ⎧                                                                            
                                                   ⇒ 
                                          ∑np ⎨diverges, if p≤1   if p =1, the series is called the harmonic series.
                                          n=1        ⎩
                                                                            ⎧                      ∞
                                                                  ∞          if  lim a  ≠0, then      a  diverges
                                                                            ⎪         n           ∑ n
                     4.        Quick Divergence Test: Given                 ⎪   n→∞                                                      
                                                                     a  ⇒ 
                                                                 ∑ n ⎨                             n=1
                                                                  n=1       ⎪
                                                                             if  lim an = 0, then No Conclusion! Do another test!
                                                                            ⎪   n→∞
                                                                            ⎩
                                                                                            ⎧   ∞                           ∞
                                                                                            ⎪if  an dn  converges  then        an converges
                                                        ∞                                   ⎪   ∫                          ∑
                     5.        Integral Test:  Given       a ,  a  >0, a  decreasing  ⇒ ⎪       c                          n=c                 
                                                       ∑ n n             n                  ⎨   ∞                         ∞
                                                       n=c                                  ⎪if  a  dn  diverges  then       a  diverges
                                                                                            ⎪   ∫ n                      ∑ n
                                                                                            ⎪   c                        n=c
                                                                                            ⎩
                                                                                                ⎧ ∞
                                                                                                ⎪     an converges,  when p <1,
                                                                                                  ∑
                                                                                                ⎪n=c
                                                     ∞                           a              ⎪ ∞
                                                                                  n+1           ⎪
                     6.        Ratio Test:  Given       a ,  a  >0  ⇒  if lim         = p then        a  diverges,  when p >1,      
                                                          n   n                                 ⎨      n
                                                    ∑                       n→∞ a                 ∑
                                                    n=c                            n            ⎪n=c
                                                                                                ⎪No Conclusion,  when p =1
                                                                                                ⎪
                                                                                                ⎪
                                                                                                ⎩
                                                                                                             ⎧ ∞
                                                                                                             ⎪    an converges,  when p <1,
                                                                                                              ∑
                                                                                                             ⎪n=c
                                                    ∞                                            1           ⎪ ∞
                                                                                n           ()               ⎪
                     7.        Root Test:  Given       a ,  a  >0  ⇒  if lim     a = lim a n = p then             a  diverges,  when p >1,      
                                                         n   n                     n          n              ⎨     n
                                                   ∑                       n→∞         n→∞                    ∑
                                                    n=c                                                      ⎪n=c
                                                                                                             ⎪No Conclusion,  when p =1
                                                                                                             ⎪
                                                                                                             ⎪
                                                                                                             ⎩
                                                            ∞            ∞                         ⎧ if  lim an = p, p > 0, p finite
                                                                                                   ⎪    n→∞ b
                     8.        Limit Comparison Test:          a  and      b , a >0, b >0  ⇒                                                       
                                                           ∑ n          ∑n  n            n         ⎨          n
                                                           n=c          n=c                        ⎪then both series converge or both diverge
                                                                                                   ⎩
                                                     ∞            ∞                                   ⎧ if  b  converges  then a  converges,
                     9.        Comparison Test:         a  and       b , a ≥0, b ≥0, a ≤b   ⇒               n                    n              
                                                    ∑ n          ∑n  n             n       n    n     ⎨
                                                                                                       if  an diverges  then bn diverges
                                                     n=c         n=c                                  ⎩
                                                                   ∞                                                      ∞
                                                                           n                                                      n
                     10.       Alternating Series Test:  Given        ()                                                     ()                     
                                                                       −1 an , if an >0, an+1 < an, lim an = 0, then          −1 an  converges
                                                                  ∑                                    n→∞               ∑
                                                                  n=c                                                     n=c